On a dotted grid, squares of many different sizes can be made by connecting four points on the grid. Below are some examples of the squares that can be made.

Now…it’s easy to calculate the areas of squares oriented like the green one, right? How about the tilted ones? You see what’s happening there…

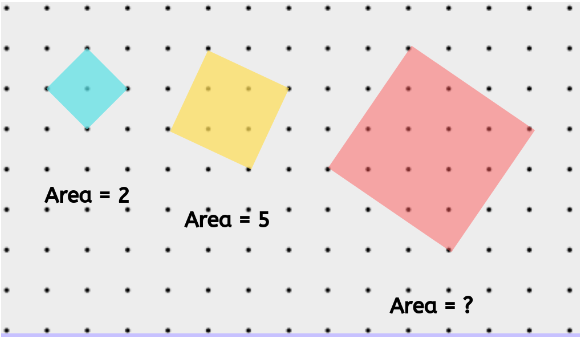
Note: the spacing between any two adjacent dots (horizontally & vertically) is 1
In a 7*7 dotted grid (given below), can you determine ALL the possible values the area of a square can take?

Challenge yourself:
Can 5 be area of a square in this grid? What about 11?
Can you find a general way to determine if a number can or cannot represent the area of a square in the grid?
Post different ways of thinking about this problem in the comments. Please try to accompany your answers with explanations. You can also email your solutions on luvformath@gmail.com
This is just an example of recursive function.
A(7) = { ( 7^2 + 0^2 ) , ( 6^2 + 1^2 ), . . . ,(3^2 + 3^2 ) } U A(6)
Where A(n) is the set of all areas possible in grid n x n .
In a 7*7 dotted grid (given below), can you determine ALL the possible values the area of a square can take?
they are 1^2=1;2^2=4;3^2=9;4^2=16;5^2=25;6^2=36;7^2=49 first types
1^2+1^2=2; 1^2+2^2=5; 1^2+3^2=10;1^2+4^2=17;1^2+5^2=26;1^2+6^2=37;
2^2+2^2=8;2^2+3^2=13;2^2+4^2=20;2^2+5^2=29;
3^2+3^2=18; 3^2+4^2=5^2(already there in first types);
4^2+3^2=5^2 (already there in first types);
note m^2+n^2=p^2; such that (m+n)<=7;
total values are 1,2,4,5,8,9,10,13,16,17,18,20,25,26,29,37 sixteen values if I did not commit any mistake in counting
You left 36 and 49
Area of red tilted square is found by findind its side;
we observe tht each side of square is formed by either 3 small segments Horizonally followed by 2 small segments Vertically or 3 small segments vertically followed by 2 small segments horizontally;
so side ^2= 3^2+2^2=13=area of square
Since the squares must have all corners on the grid, we can think of them as special kites whose area are given by diagonal squared over 2. For the red one we have diagonal running 5 dots over and rising 1 dot, so the diagonal is sqrt(5^2+1^2) =sqrt(26). Squaring that divided over 2 is area 13. Then the question becomes what possible arrangements of diagonals you can form here.
That’s an interesting way to look at it in terms of diagonals. Taking this further, how do we approach the challenge question through this? “Given a number, how do we determine if it can or cannot represent area of a square on the grid”